LeetCode 0994 - 腐烂的橘子

📖 题目描述

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；

值 1 代表新鲜橘子；

值 2 代表腐烂的橘子。
每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：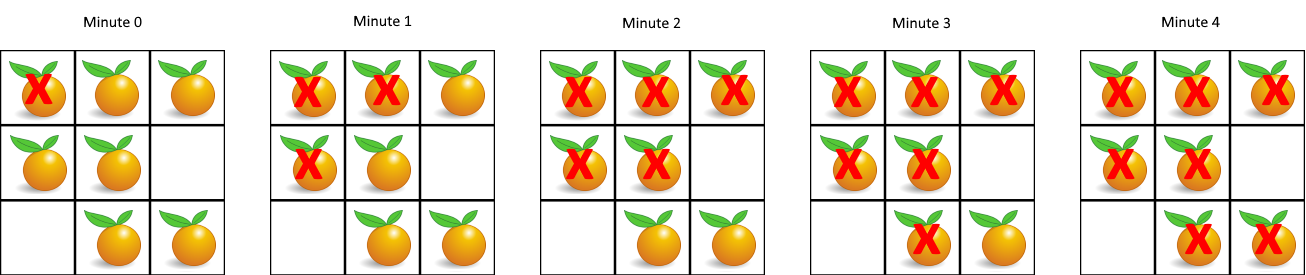

输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4
示例 2：
输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行，第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。
示例 3：
输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

核心问题：如何在每分钟内模拟腐烂橘子的传播过程，并判断所有新鲜橘子是否都能在有限时间内被腐烂，如果可以则返回所需的最小分钟数，否则返回 -1。

💡 解题思路

🔎 思路概览（一句话总结）

使用多源广度优先搜索（BFS）从所有腐烂橘子同时开始扩散，逐层传播腐烂状态，直到无法继续或所有新鲜橘子被腐烂。

问题建模为图传播问题：
- 将网格视为一个图，橘子之间的传播关系可以看作图中结点之间的边（上下左右相邻）。
- 腐烂橘子的扩散过程等价于图中的逐层 BFS 遍历，每一层代表一分钟。
使用多源 BFS：
- 所有初始的腐烂橘子同时开始传播，相当于图中多个起点的 BFS。
- 每轮 BFS 扩展一步，相邻的新鲜橘子腐烂并入队。
逐步推进时间：
- 每完成一层 BFS 扩展（即当前队列中的所有橘子处理完），分钟数加一。
- 直到没有可传播的橘子或所有新鲜橘子腐烂完。
终止条件与结果判断：
- 如果在 BFS 结束后还有未被腐烂的新鲜橘子，说明存在无法被感染的孤立区域，返回 -1。
- 否则，返回传播所经历的分钟数。

利用 BFS 的分层特性自然模拟“时间的流逝”，将局部传播扩展为全局感染。

🧩 解法详解

将所有初始为2的腐烂橘子位置加入队列，作为 BFS 的起点（多源 BFS)；
同时统计初始为1的数量（新鲜橘子数）；
每进行一轮 BFS （每分钟），将队列中所有腐烂橘子对四个方向进行拓展：
1. 如果发现邻接的新鲜橘子`grif[x][y] == 1’：
  1. 腐烂它（变为 2），并加入队列；
  2. 新鲜橘子数减 1.
直到队列为空，统计所需的分钟数；
如果最后仍有新鲜橘子存在，返回-1，否则返回分钟数。

📈 复杂度分析

m为网格行数，n为列数。

时间复杂度：O(m * n)，在 BFS 过程中，每个格子最多访问一次（因为橘子一旦腐烂，不会再次入队）。每个腐烂的句子在上下左右最多拓展 4 次邻居，但不会重复，因此最多处理m * n个格子。
空间复杂度：O(m * n)，队列中最多同时存储所有格子的坐标，最坏情况是所有橘子都腐烂入队。

✅ 代码实现

import java.util.LinkedList;  
import java.util.Queue;  
import java.util.Scanner;  
  
public class RottenOranges {  
    // 定义四个方向的移动数组，分别表示：上、下、左、右  
    static int[] dx = {-1, 1, 0, 0};  
    static int[] dy = {0, 0, -1, 1};  
  
    // 主算法函数：计算所有新鲜橘子腐烂所需的最小分钟数  
    public static int orangesRotting(int[][] grid){  
        int m = grid.length;  // 网格行数  
        int n = grid[0].length;   // 网格列数  
        Queue<int[]> queue = new LinkedList<>();  // 用于 BFS 的队列，存储腐烂橘子的位置  
        int fresh = 0;   // 新鲜橘子的数量统计  
  
        // 遍历整个网络，初始化队列和新鲜橘子计数器  
        for (int i = 0; i < m; i++){  
            for(int j = 0; j < n; j++){  
                if (grid[i][j] == 2){  
                    // 将初始腐烂橘子的位置加入队列  
                    queue.offer(new int[]{i, j});  
                }else if(grid[i][j] == 1){  
                    // 统计新鲜橘子的总数  
                    fresh++;  
                }  
            }  
        }  
  
        // 如果没有新鲜橘子，说明无需传播，直接返回 0 分钟  
        if(fresh == 0) return 0;  
  
        int minutes = 0; // 用于记录传播所需的分钟数  
  
        // BFS 开始：每轮表示一分钟  
        while(!queue.isEmpty()){  
            int size = queue.size(); // 当前轮要处理的腐烂橘子数量  
            boolean changed = false; // 本轮是否有新鲜橘子被腐烂  
  
            // 处理当前队列中所有腐烂橘子  
            for(int i = 0; i < size; i++){  
                int[] curr = queue.poll(); // 当前腐烂橘子的位置  
                int x = curr[0], y = curr[1];  
  
                // 向四个方向拓展  
                for (int d = 0; d < 4; d++){  
                    int nx = x + dx[d]; // 新位置的行  
                    int ny = y + dy[d]; // 新位置的列  
  
                    // 检查边界是否合法并且该位置是新鲜橘子  
                    if(nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == 1){  
                        grid[nx][ny] = 2; // 将新鲜橘子腐烂  
                        fresh--; // 新鲜橘子数减一  
                        changed = true; // 标记本轮有橘子腐烂  
                        queue.offer(new int[]{nx, ny}); // 将新腐烂的橘子加入队列  
                    }  
                }  
            }  
  
            // 如果本轮有橘子腐烂，则分钟数加一  
            if (changed) minutes++;  
  
        }  
  
        // 判断是否所有新鲜橘子都腐烂了  
        return fresh == 0 ? minutes : -1;  
    }  
  
    // 主函数：读取输入，调用算法函数并输出结果  
    public static void main(String[] args) {  
        Scanner sc = new Scanner(System.in);  
        int m = sc.nextInt(); // 输入行数  
        int n = sc.nextInt(); // 输入列数  
        int[][] grid = new int[m][n];  
  
        // 读取网格输入  
        for(int i = 0; i < m; i++){  
            for (int j = 0; j < n; j++){  
                grid[i][j] = sc.nextInt();  
            }  
        }  
  
        // 输出结果  
        System.out.println(orangesRotting(grid));  
    }  
}